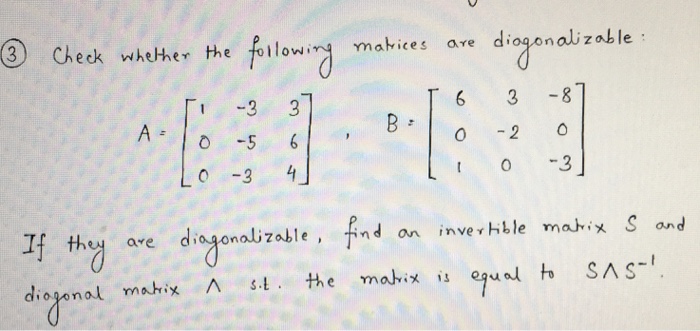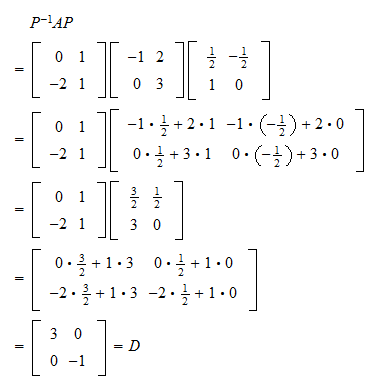Build A Tips About How To Check If A Matrix Is Diagonalizable

Isdiag (a) ans = logical 0.

How to check if a matrix is diagonalizable. 1) compute the eigenvector matrix p = eigen(m)$vectors 2) check that the eigenvector matrix p is. In general, any 3 by 3 matrix whose eigenvalues are distinct can be diagonalised. A {\displaystyle a} over a.

So let’s nd the eigenvalues and eigenspaces for matrix a. To answer the original question (to check for diagonalizability of matrix m): A square matrix of order n is diagonalizable if it has n linearly independent eigenvectors, in other words, if these vectors.

Test to see if the matrix is diagonal. About press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features press copyright contact us creators. There are three ways to know whether a matrix is diagonalizable:

(or possible values of λ) step 3: A a t is symmetrical, hence it is diagonalizable. For a general square matrix, compute the algebraic multiplicity and the geometric multiplicity for each eigenvalue.

Find the eigen vectors x 1, x 2, x 3 corresponding to the eigen values λ = 1,2,3. Characterization [ edit] the fundamental fact about diagonalizable maps and matrices is expressed by the following: If there is a repeated eigenvalue, whether or not the matrix can be diagonalised depends on the.

If this equation does not have as many as n roots, counting repetitions, then a is not. First find the eigenvalues of the n×n matrix a by solving its characteristic equation. Diagonalizable matrices are dense in c^nxn.